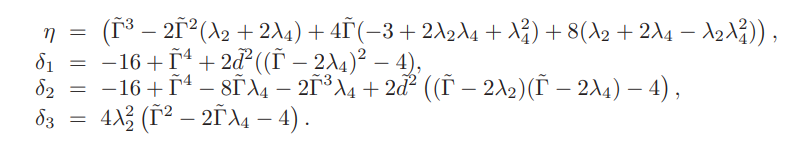This paper is available on arxiv under CC 4.0 license.
Authors:
(1) Amit Kumar Chatterjee, Yukawa Institute for Theoretical Physics, Kyoto University & Department of Physics, Ramakrishna Mission Vidyamandira;
(2) Satoshi Takada, Department of Mechanical Systems Engineering and Institute of Engineering;
(3) Hisao Hayakawa, Yukawa Institute for Theoretical Physics, Kyoto University.
Table of Links
- Introduction
- Model and Protocol
- Different Regimes in d˜− Γ˜ Plain and Multiple QMPE
- QMPE in Region (d): Second-order Ep
- QMPE in Region (a1): Oscillations
- Summary
- Appendix A: Eigenvectors of L in region (d)
- Appendix B: Eigenvectors of L in region (a1)
- Appendix C: QMPE in region (b): purely exponential relaxation
- Appendix D: QMPE in region (e): 3rd order EP
- References
Appendix A: Eigenvectors of L in region (d)
In this Appendix, we give the explicit expressions for the right eigenvectors |rki and left eigenvectors hℓk| of the Lindbladian [Eq. (2)] in region (d) [Sec. IV], where k = 2, 3, 4. The right and left eigenvectors corresponding to the zero eigenvalue i.e. the steady state. have already been provided in Eq. (3). Below are the expressions for the right eigenvectors
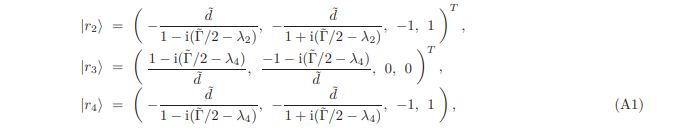
where the superscript T denotes transpose. The left eigenvectors are obtained to be
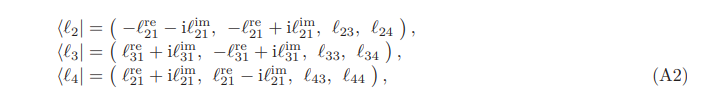
where the elements lkn are explicitly given by
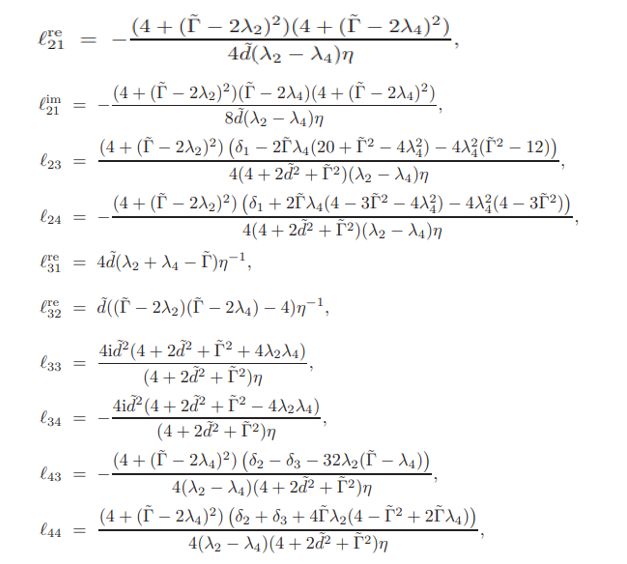
where the eigenvalues λ2 and λ4 are given by Eq. (12) and the parameters η, δ1, δ2, δ3 used in Eq. (A3) have the following forms