Multiple Quantum Mpemba Effect: Exceptional Points and Oscillations: Appendix C: QMPE in Region (b)

5 Mar 2024

This paper is available on arxiv under CC 4.0 license.

Authors:

(1) Amit Kumar Chatterjee, Yukawa Institute for Theoretical Physics, Kyoto University & Department of Physics, Ramakrishna Mission Vidyamandira;

(2) Satoshi Takada, Department of Mechanical Systems Engineering and Institute of Engineering;

(3) Hisao Hayakawa, Yukawa Institute for Theoretical Physics, Kyoto University.

Table of Links

Appendix C: QMPE in region (b): purely exponential relaxation

In this Appendix we discuss QMPE in region (b) of Hatano’s model that contain eigenvalues 0, −iλ2, −iλ3, −iλ4 obeying 0 < λ2 < λ3.

1. Density matrix elements

FIG. 13. The figures (a) and (b) show nature of QMPE in energy and von Neumann entropy in region (b), respectively, for the same parameters exhibiting double QMPE in ρgg(t) in Fig. 12(b). We observe that although energy shows double QMPE (figure (a)), the von Neumann entropy exhibits single QMPE only (figure (b)).

where

In Fig. 12(a), we present the intersection time solutions denoting QMPE in ρgg(t) as functions of the control parameters ˜dI and ˜dII. Indeed, we observe that there are parameter regions where both t˜+ and t˜− are positive and finite, indicating double QMPE. Other regions have only one intersection time, either t˜+ and t˜−, implying single QMPE. To demonstrate double QMPE, the Fig. 12(b) exhibits a specific example of double intersection in ρgg(t). However, the two copies become close enough so that the second intersection (shown in inset of Fig. 12(b)) is weak in magnitude and hard to detect.

2. Energy

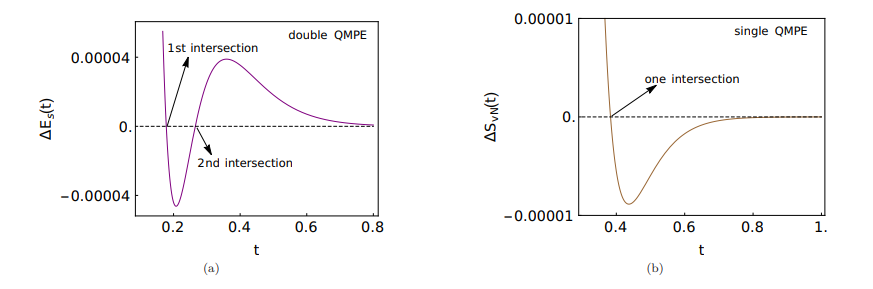
We look for solutions to ∆Es(t) = 0, which can give to single or multiple QMPE depending on the number of positive finite intersection time solutions. The Fig. 13(a) shows that the average energy exhibits double QMPE indicated by the twice zero intersections of ∆Es(t), for the same set of parameter values producing double QMPE in ρgg(t) in Fig. 12(b).

3. von-Neumann entropy

Here we ask if the entropy, like density matrix and energy, also exhibit double QMPE for the same set of parameters used in Figs. 12(b) and 13(a). However, in Fig. 13(b), we observe that the entropy difference ∆SvN(t) between two copies intersect zero only once, giving rise to single QMPE instead of double QMPE.

4. Temperature

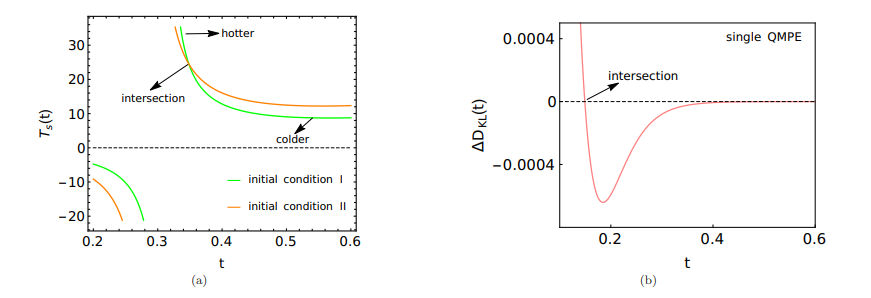
In Fig. 14(a), we present the time evolution of temperatures for the two copies I and II, one initially starting as hotter with respect to the other. We observe that the temperatures of the two copies intersect each other i.e. the hotter becomes colder and vice versa. Notably, unlike ground state probability [Fig. 12(b)], energy [Fig. 13(a)] that can exhibit double QMPE, we have observed only single QMPE in temperature. If observation of multiple QMPE is possible or not with purely exponential relaxations, remains an open question.

5. Kullback-Leibler divergence

Here we study the possibility of QMPE in KL divergence for the same parameters used to explore thermal QMPE in Figs. 14(a). The Fig. 14(b) shows QMPE in KL divergence, however the intersection time corresponds to negative temperatures in Fig. 14(a).